Kicks - Static Electricity

 

During the 2013 Betfair World Snooker Championships the match between Graham Dott and Shaun Murphy was interrupted due to Graham Dott having suffered several sever static electic shocks.

The Match officials overcame the problem by damping the carpet with water from a hand spray, which seem to have the desired effect.

Perhaps some research instigated by Norman Clare, into the possibility that static electricity could be the cause of 'KICKS' may have reduced or even removed the problem especially the comments on clothing, shoes and the carpet.

For some reason Norman Clare never published the research but his son Peter, prompted by the Dott situation, thought it was time that the work was available.

The experiments and research was carried out in 1987 in the Billiard Room of the long established 'Gentleman's Club called the Lyceum (now sadly no longer in existence), when it was situated in Paradise Street. Norman was a member and in fact was President of the Club on two occasions and so was able to have permission to use one of the four Ashcroft Billiard tables that were in the Billiard Room.

The report follows :-

STUDY REPORT

E. A. CLARE & SON Ltd.

 STATIC ELECTRICITY AND THE "KICK" PHENOMENON

JULY 1987

 PREPARED BY :-

COMPUTING IN BUSINESS

SUITE 40,

WIRRAL BUSINESS CENTRE

GORSEY LANE

BIRKENHEAD, L41 1JW

 REF NO. BTAS 31899

CONTENTS

 

1. INTRODUCTION TO REPORT 

1.1 Terms of reference

1.2 Confidentiality

2. INTRODUCTION TO STATIC ELECTRICITY

 3. COMPANY PROFILE

4. MATERIALS ANALYSIS 

5. FIELD EXPERIMENTS

5.1 Introduction to the "KICK" effect

5.2 Experimental work

5.3 Analysis of field ant motion effects

 6. CONCLUSIONS AND RECOMMENDATIONS

Appendix A References

Appendix B Basic programs used in evaluation of analyses.

© 1987-2013 -E.A. Clare & Son Ltd.

1. INDUCTION TO REPORT

1.1 Terms of Reference

Computing In Business has been retained by E.A. Clare & Son Ltd T/A Peradon (and Fletcher Ltd.), manufactures of billiard/snooker cues and accessories, to investigate and report upon the nature and values of static "build up" on billiard and snooker tables taking cognizance of environmental surrounding. The prime objective of the study is to evaluate whether or not the measured levels of static would be of significant magnitude to produce the phenomenon known as "kick".

The study has attracted financial support under the department of Trade and Industry's Business and Technical Advisory (BTAS) scheme (project reference No. 31899). Computing in Business is obliged to include in the report the following DTI terms and conditions applicable to projects undertaken under the BTAS scheme.

"Whilst every care has been taken to ensure that the advice in this report is correct, neither the Secretary of State for Trade and Industry, the Secretary of State for Defence nor Salford University Business Services Ltd. Will accept responsibility for loss, damage, etc., howsoever arising, occasioned by the implementation of such advice. No liability should rest upon the Secretary of State for Trade and Industry, the Secritary of State for Defence, nor upon Salford University Business Services Ltd. If implementation of any of the advice contained in this report would involve use of patents and like protection not held by your Company. In such circumstances appropriate legal advice should be sought.

It is a condition of payment by the Department of Trade and Industry for work done in connection with this project that a copy of the report on the project shall be supplied in confidence to the Department of Trade and Industry.

If, as a result of the advice and recommendations contained in this report, you are proposing to purchase any paint or equipment, you are strongly advised, before entering into any commitment, to contact your regional office of the Department of Trade and Industry in order to ascertain the up-to-date position regarding government grant to which your company may be entitled."

1.2 Confidentiality

The information contained in this report, along with such information as may be provided during discussions with parties other than Peradon is to be regarded as strictly confidential & can only be used with the permission of E.A. Clare & Son Ltd.

2. INTRODUCTION TO STATIC ELECTRICITY

2.1 General

Though one of nature's most widely displayed phenomena, static electricity is among the most capricious. Many of its manifestations are familiar to all of us, in the form of lighting and its aftermath thunder. It was the Greeks who first noticed electrostatic energy when they rubbed amber against cats fur and an electrostatic charge resulted. They names this effect tribos charge which results from bringing together of two different materials and then separating them.

Static charged have caused little or no serious problems to industry in the past. However, in the last ten years modern society has rapidly come to depend on electronic devices. These devices are based increasingly on low-power logic silicon chips which are extremely susceptible to electro-static discharges. Moreover, at present even more sensitive technologies are being developed, typically silicon-on-sapphire (S O S) and Gallium Arsenide (GaAs).

 Static discharge can damage devices at five basic stages:

 1) within the semiconductor manufacturer's plant;

2) at the distributor's site;

3) within the company which is using the devices to build a product;

4) in normal operation at the end user's site;

5) during service and repair.

In a typical office environment static electricity can be generated in many ways; the most common causes are frictional contact and movement between the following surfaces and/or items which may be found in many offices:-

1) work surfaces which are waxed, painted, varnished, or consist of natural plastic or laminate.

2) Floors of sealed concrete, waxed or varnished wood, vinyl tiles and all carpets containing natural or man-made fibres, especially nylon.(It would be interesting to know what the carpet at the Betfair 2013 World Snooker Championships was made of)

3) Chairs/clothes; where operators wearing clothing made of man-made fibres move to and fro on an insulated chair.

4) All types of common articles left on desk tops, including expanded polystyrene, envelopes, plastic bags, trays, plastic folders, binders and coffee cups.

In general the level of static produced increases considerably as the surrounding air becomes drier, which is reflected in a fall in relative humidity. However, the situation is complicated by the relationship between humidity and temperature; colder air holds water vapour less well then warm air, and consequently low temperatures imply low humidity and greater static problems. (Under TV lights the atmosphere is drued out so the humidity is low) 

Typically in the summer, when the relative humidity is between 60% - 80%, walking across a nylon carpet will generate approximately 1,500 Volts. However, in winter, when the relative humidity has fallen to between 10%-25%, the same movement will generate voltages in excess of 30,000 Volts. At standard office temperatures of 20-25 degrees centigrade, it may safely be said that static problems will certainly occur if the humidity, for whatever reason, remains consistently below 40%.

Typical voltages causing shocks to operating staff are in the order of 3,000 Volts or more. These voltages are also sufficient to cause data loss on a computer system.

It should be noted that when computer systems are subjected to static discharge the screen will normally go blank, the system will reset itself, and data currently being worked upon will be either lost or corrupted. These symptoms are often attributed to mains interference, spikes, or other such factors. However, the most likely cause is electrostatic discharge.

Certain types of carpets, chairs and other office equipment are referred to as having "anti-static" properties, meaning that under normal conditions movement on or around them will not create static electricity. However, such equipment and carpeting is extremely susceptible to dust and dirt impregnation which reduces its anti-static effectiveness and has the further disadvantage of offering no common earth path for discharge.

The maximum protection from unwanted static can be gained only from conductive materials which can be earthed in a safe manner.

The human Body As A Capacitor

Capacitance measurements for the human body range from 80 pfd (pico Farads) to 500 pFd at the farthest extreme.

Women usually have higher capacitance than men due to the thinner soles on their shoes.

Thus, walking across a floor or carpet will charge up a human's capacitance. Charging currents lie between hundreds of pico amps and a few micro amps and total charge ranges from 0.1 to 5 micro coulombs.

Calculating the voltage V = Q/C for a 150 pFd person charged with 3 micro coulombs produce a sum of 20,000 volts.

Raising an arm changes the stored voltage by 100v. Standing up changes the stored voltage by 1000 to 1500v. Grounding oneself momentarily, then lifting one foot off the floor will increase the stored voltage by 1500 to 2000v.

In an extreme case a person can charge up to 40,000 volts. Above this figure a corona discharge effect self-limits the voltage to this figure.

3. COMPANY PROFILE

Peradon is a market leader in the UK for the manufacture of billiard/snooker cues and tips.

From a Liverpool site it manufactures cue tips from selected leather for the UK and export markets and carries a wide selection of snooker and billiards accessories which are factored.

An associate company within the group, E.A. Clare and Son (Trading as Thurston, Peradon & Drakes Pride) are leaders in the field of snooker and billiard table manufacture.

For many years there has been a problem with the phenomenon known as the "kick" which causes the cue ball and object ball to display different characteristics from normal in certain instances of impact.

The phenomenon is infrequent and erratic but due to the high current level of commercialisation of the game, it is now assuming significant importance in top level tournaments.

Very little study has previously been undertaken in this area and the company could benefit greatly from new products and/or services should a solution to this phenomenon be found.

4. MATERIALS ANALYSIS

As previously described in the "Introduction to Static Electricity" the surface conductivity of materials plays an important part in the generation and dissipation of static electricity. The following table gives a general indication of the electrical properties of materials and their conductances.

MEASURED SURFACE RESISTIVITY OF SNOOKER TABLE COMPONENTS ACCESSORIES.

 

Material	Surface Resistivity
Slate Bed	10 10  Megohms
Table Cloth	10 14 Megohms
Wood Surround	10 8  Megohms
Rubber Cushion	10 15 Megohms
Chalk	10 12  Megohms
Snooker Balls	10 11  to 10 13 Megohms
Cue Shaft	10 8 Megohms
Cue Tip	10 11 Megohms

 

 

All readings were taken at 65% RH and 19.4 ⁰C.

From the above readings it can be seen that the materials used in the manufacture of snooker tables have surface resistivities in the range 10 ¹⁰ to 10 ¹⁵ ohms per square; the exception being the snooker cues which have surface resistivity of approximately 500 megohms for both Ash and Maple types, with the Ebony and base measuring 10,000 megohms.

The readings obtained indicate that surface resistivity levels of this magnitude will not afford fast dissipation of any static charges generated as indicated in Section (5). Typically decay rates were measured at 34 to 137 seconds for a charged ball on baize.

The surface resistivity of the ash and maple cues measured at 500 Megohms will allow a transfer of charge from the person holding the cue to the ball.

5. Field Experiments

5.1 Introduction

Please note that bibliographic references (*) in this section of the report are detailed in Appendix A.

Evidence exists that the "kick", an unexpectedly dull impact between cue ball and object ball causing both balls to move unpredictably in both direction and velocity, can be caused by an interposing substance or layer at the point of impact of cue and object balls (1). To date, the most accepted postulate has been the presence of cue chalk on this impact point; a previous experiment has seemingly confirmed this effect by deliberately placing layers of paper or fine cloth at the impact point and observing motion similar to that seen when the "kick" occurs. (2). There is, however, much anecdotal or circumstantial evidence to suggest that cue chalk is by no means the sole cause of "kick" behaviour. For example, it is noted that some players are particularly susceptible to the "kick"; as are certain tables, or types of cue, or sets of balls, and even climatic variations have seemed to play a part (2). While mathematical analysis of the motion and collisions of snooker and billiard tables have been carried out (4) (5), the prevalence of the "kick" effect has not been of sufficient volume or repetition to warrant any analysis of its effects.

If the deduction is made from the previous research that the "kick" is due to a sudden frictional force at the point of impact (similar to the force caused by a layer of paper or chalk at the impact point), it may be postulated that the reduction in rotational velocity is due to the effects of local charge on both balls and table, especially in the case of a slow shot. The following summaries of experimental work and analysis of the dynamics of ball motion will explore this hypothesis.

5.2 Experimental Work

The experimental conditions were those much favoured by many scientific researches during relaxation - a standard snooker table, cue, and balls, in carpeted environment. Relative humidity was measured at 59.7% and temperatures at 19 degrees centigrade. Measurements of electric field were carried out using a field-mill type of meter, connected to an x-y plotter when dynamic effects were being observed. Resistivities were measured using an electronic meter capable of resolving 100,000 Megohms.

5.2.1 Resistivities

As is normal, the cues consisted of an ebony base and a wooden shaft. The resistance of both types of cue wood made available, Ash and Maple, was approximately 500 Megohms, and that of the ebony base was of the order of 10,000 Megohms. The table surface resistivity was greater than 30,000 Megohms. A check on the resistance across the diameter of the balls showed that the black was noticeably more resistive (30,000 Megohms) than the other balls, which all showed approximately 10,000 - 20,000 Megohms. However, the presence of moist air on the surface of any ball could reduce its measured resistance to 500 Megohms.

5.2.2 Initial experiments and the electrostatic effects of different ball colours

To determine the approximate size of field effects seen in snooker play, a single ball was struck around the table to return to the player after 5-6 collisions with side cushions, and the field meter used to detect the presence of electrostatic charge, if any, on the ball. This confirmed the presence of static charge on the balls; although a residual of up to 700 V/m could be occasionally detected before the shot. The field close to the ball surface after the shot was below 5 KV/m only in one case, and occasionally much higher. At this point, as can be seen from the results tabulated below, it was noticed that certain colours could repeatably produce hight charge effects than others.

 

Colour	Field at ball surface (KV/m)
White	-0.7
Red	-7
Yellow	-11
Green	-5
Brown	-5
Blue	-12
Pink	-6
Black	-12

A more precise variant of this experiment was conducted, using the system shown in figure 1, overleaf. Each colour was used several times; the subsequent table records average values of maximum measured field during each pass of the ball below the sensor. In some cases, a large variation was recorded, and this is expressed in the table.

  

Colour	Max. field 2cm above ball forward                 return
White	-1.4                            -0.7
Red	-1.5                            -1.7
Yellow	-1.0                      -1.3 to -2.2
Green	-1.1                      -1.5 to -3.0
Brown	-1.2                      -1.0 to -2.2
Blue	-1.5                         - 2.7
Pink	-1.6                         -1.5
Black	-1 to -2               -1.5 to -5

Thus, the colour effect was confirmed, and it was found that a cushion bounce could increase ball charge by up to 200%. This latter effect was, however, not readily repeatable, and a large variation existed between the occasional hight values of 500% for this increase and the more usual 30% - 50% changes. It was noted that the largest variations in this experiment occurred with the brown ball, where on one occasion a reading of -14 KV/m was obtained.

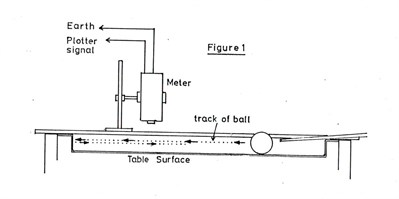
picture of actual set up for the experiments

 5.2.3 The effect of the type of shot

The same apparatus as in 2.2 was then used to investigate the effect of fast shots, slow shots, screw-back, with the black ball as cue ball. From the results shown in the table below, it can be seen that the type of shot has an effect in most cases and that the strength of shot also is a factor in the size of charge produced on the ball.

 

Type of shot	Field produced
Screwback	-4 to -6
Side	-1 to -2.6
Screw	-1.5 to -1.6
Slow screw	-2 to -3
Top	-0.7 to -1
Stun (shortrange)	-0.4 to -0.6
Stun (long range)	-0.9 to -1.2

 5.2.4 Table Charge

By paying a ball past the sensor of the field meter, the effect of charge left on the baize was noted as being of opposite polarity to the charge on the ball, and of between 10% and 30% of the magnitude of ball electric field. This charged "track" extended by approximately a centimetre around the line of ball movement.

In addition to this local charge density it was noted that an overall charge density on, and close to, the table could be generated from the presence and movement of players around it.

5.2.5 Decay of charge

Decay times of all the above phenomena were noted. While initial decay of ball charge was of the order of 10% per second, this rapidly settled to an overall decay time of 30 -15 seconds to discharge.

5.3 Mathematical analysis of the changed caused by the presence of electrostatic charge on cueball and object ball.

5.3.1 Velocity changes due to electric field effects between charged cue ball and object ball

The assumptions in the following analysis are as follows:-

(a) - the cue ball is hit in such a way as to induce perfect rolling motion with no trace of skid.

(b) - an electric charge is picked up by the cue ball on impact of the cue, and no charge is lost or gained during cue ball travel.

(c) - the charge on the ball behaves as a point charge.

The condition (a) is one which can be readily achieved by a slow shot, as shown by previous researches (5), and can even be created on a fast shot if the cue impact point is correctly chosen. Condition (b) is probably an over-simplification, but serves to underline the fact that in practice, some extra charge may be created by friction between table and cue ball or between side cushion and cue ball. Condition © is almost certainly an over-simplification, but probably valid at separations of cue ball and object ball of greater than a few millimetres.

To find the size of the charge held by the cue ball if the voltage of its surface us known, the standard formula is used:-

      

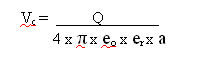
where: a = distance between point charge and measured voltage

Q = size of point charge

V_c = measured potential at distance a from point charge

e_o = free space permittivity

e_r = relative permittivity of cue ball

Simple transposition gives :-

         Q = V_c x 4 x π x e_ox e_rxa

from experimental data, the approximate voltage given to the cue ball is 100v, the ball radius being 3cm., and the assumption may be inserted that the relative permittivity of the polymeric resin of the ball is 4. This gives, when these figures are inserted into the above formula a charge of 1.3 x 10 ^-9 coulombs on the cue ball; a figure not unreasonable given that a human (of approximate 1000 pf capacitance to earth) with a 100v potential may store 10 ^-7 coulombs (6).

If the voltage of the object ball is V_o , the size of the field produced by the object ball (assuming it is a point charge) is, from another standard equation:-

          

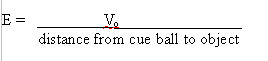
Thus, if the initial ball separation is s, and the distance travelled is d, this may be formalised slightly:-

      

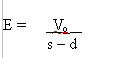
At any point in the cue ball travel, the force exerted by the field on the charged ball is

       F = Q x E

Thus, the energy loss corresponding to work done against the field by bringing the balls closer together is, at any instant in the ball motion,

Work done = Force x distance moved by the force

                   = Q x E x d

Inserting the previous formulae :-

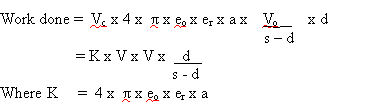
Therefore, the total work done between the initial cue ball position and the current position d is found by the integration, over the distance d,

     

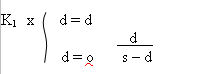
where the quantities K, V_o, and V_c, which do not vary with distance, have been combined into K₁. The integral is standard readily found in mathematical reference books (3), and has the value :-

     [s - d - s x 1n(s-d)]

Once the limiting values are inserted, some algebraic manipulation gives

     

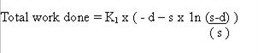
To enable comparisons with the original kinetic energy of the cue ball, the kinetic energy of a rotating sphere assuming no skid component is, form the standard formula :-

 

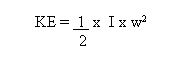
Where I = moment of inertia of a rotating sphere

           w = rotational velocity

The moment of inertia of a sphere, I, is another standard formula,

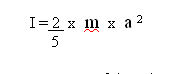
Where m = mass of the sphere

           a = radius of the sphere

The angular velocity is obtained by

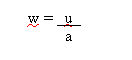
where u = linear velocity of the edge of the ball

           a = radius of the ball

Substitution of the definitions given for the moment of inertia and the angular velocity gives :-

    

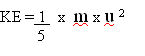
Thus, if the energy change due to work done by the electrical effects is expressed as a change in ball velocity, to the value u' , the above equations may be combined as :-

 

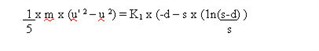
Further algebraic manipulation gives the result that the fractional velocity change u'/u, is given by

   

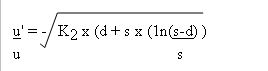
Where all constant terms have been combined into K :-

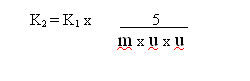
5.3.2 Discussion of velocity change effects

It must, at this point, be noted that the asymptotic behaviour indicated by the logarithmic term is unrealistic, since it indicates the fairly elementary fact id electrical theory that two charges of the same polarity would need an infinite amount of work to overcome their repulsion and superimpose. Thus, the first numeric substitutions into this equation concerned the effect of reductions in the size of the final separation used as one of the limits of integration.

Using ball voltages of 500 volts, initial separation of 30cm. , and an initial cue ball velocity of 10cm/second, the following data resulted from numeric substitution into the program shown in Appendix b :-

 

Final d value	% change in velocity
27 cm.	0.3
29 cm.	0.6
29.9 cm.	1.2
29.99 cm.	1.7
29.999 cm.	2.3
29.9999 cm.	3.4

Since the close contact effects of like charges on snooker balls are not easily predicted, but are unlikely to occur at separations greater than 1cm, the 29 cm. mark is used as the standard integration limit in the following numeric investigations. It must be noted, however, that the size of velocity loss may be up to five times larger than this limit shows.

The effect changes in the initial cue ball velocity is shown below, using an initial separation of 30cm. and 500V on each ball :-

 

Initial velocity	% change in velocity
10cm/sec.	0.6
5cm/sec.	2.4
2cm/sec.	14.2

Clearly, slower shots are highly vulnerable to electrostatic effects.

5.3.3 Effects of velocity change on object ball trajectory

The error angle caused by the changes in one component of linear velocity may be estimated by the following method, using the diagram in Figure 2. if, as an example, a quarter - ball shot is undertaken at the separation between cue and object balls of 30 cm., the angle between line AA (joining both ball centres) and the desired direction of the cue ball can be calculated by :-

 

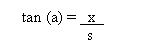
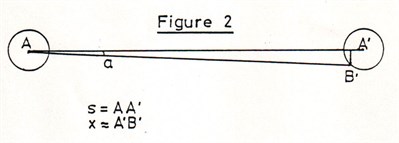
Where x is the distance between the aim point for a straight shot and that for a quarter - ball shot. A good estimate for x is half the ball radius; inserting numeric values, the angle a is therefore, in this case, 2.86 degrees.

The linear velocity of the ball has two components with respect to AA' ; ux, along AA' which is attenuated by electrical field repulsion to a value vx, and uy, normal to it, which is not deflected. If the final angle of approach is a', the rekation between a and a' can be expressed as :-

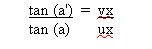
A decrease of 10% of the component parallel to AA' gives the value 0.9 to the right side of the above equation. This gives a' as 2.57 degrees, and the error angle as the difference between a and a' is 0.28 degrees.

The diagram in Figure (3) is a simplified version of that used by a previous researcher (4) into dynamics of collision between billiard balls, who also supplies a formula for the calculation of the angular error of the object ball at the target position ;-

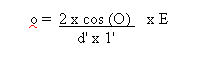
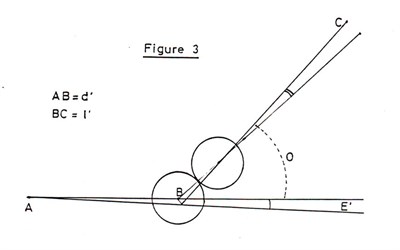
Where O = angle between error- free cue ball direction and object ball direction

E = error angle, between desired and actual cue ball direction

d' = distance from cue ball to object ball

1' = distance from object ball to target position

For the case of quarter - ball shot, the angle O is approximately 45 degrees. The product of d' and 1' is maximised when these are equal; 1' is therefore set at 30 cm. These numeric values, if substituted into the above equation, give a value of 4.4 degrees to 0. the linear error is simply 0 x 1' if 0 is expressed in radians; for the shot under discussion, this gives an error of 2.3 cm.

It is, therefore, clear that if the electric field causes a velocity change of 10%, an error of greater than a ball radius is induced in a fairly short quarter - ball shot. This is, however, seldom fatal to the desired effect of a snooker shot even at top levels of play. It is interesting to note that the effect is similar in size to that produced by the "nap" of the table bed cloth, and may in some situations be mistaken for it.

5.3.4 Effects of the last quarter - turn of the cue ball before impact

The previous sections considered the cue and object balls as point charges, however, experimental evidence tends to indicate that when a ball is rubbed on the table surface, the charge on the ball is localised to the region of contact between ball and table. This implies that any charge given to the ball from the cue is similarly localised. Thus, motion of the charge is not linear, but consists of a rotational pattern, and although the integrations over cue ball travel distance in the previous work would become more complex, it is expected that displacements above and below the line of motion of the cue ball centre would be cancelled by the integration. This cancellation effect is expected to break down at close distances between cue ball and object ball, and the following analysis therefore explores the effect of point charges on the surfaces of the balls on rotational velocity.

The simplified situation shown in Figure 4 is assumed. Initial separation s of the charges at B and E can readily be found, by using the right-angled triangle BCE. The distance CE is the linear travel corresponding to rotation of the last quarter - turn, i.e. a + πa/2 where a is the ball radius. The distance BC is equal to the ball radius a.

  

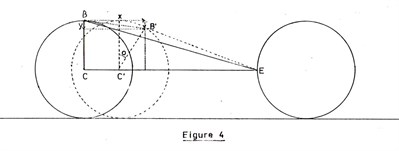
When the ball has moved to a new position centred on C', the new positio of the charge is b' , having moved by the amounts marked as x and y on the diagram. This is due to the linear translation CC' and the angular movement o.

From the diagram, it is clear that the distance y can be expressed as :-

      y = a x (1 - sin (o) )

 The expression for x is ;-

      x = CC' + (a x coz (o) )

CC' is equal to the distance moved by the arc contained by the angle o, and if o is expressed in radians the above expression becomes :-

      x = a x (o + cos (o) )

Thus, both positional variables have been expressed in terms of the angle of rotation o.

It is now assumed that the identity below is valid:-

Total work done = work done against + work done                                                        against field           x component             y component

and, from the previous section,

 

where the constant K is given the value which sets the charge on the cue ball to 10 ^-9 coulombs, as was the case in the previous analysis. This is done by transposition of;

  Q = K x V

if V is taken as 500 Volys, K has the approximate value of 2 x 10 ^-12.

Thus, each component may be evaluated in turn, using the following method of integration over one variable with respect to another :-

 

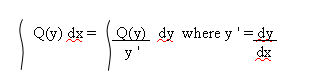
In the case of y component, the main equation for integration, after some algebraic manipulation, consists of;-

  

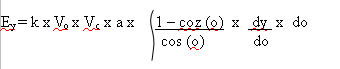
From the definition of the relationship between y and o given earlier, the differential term is readily extracted, and the above equation becomes

   

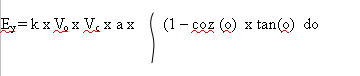
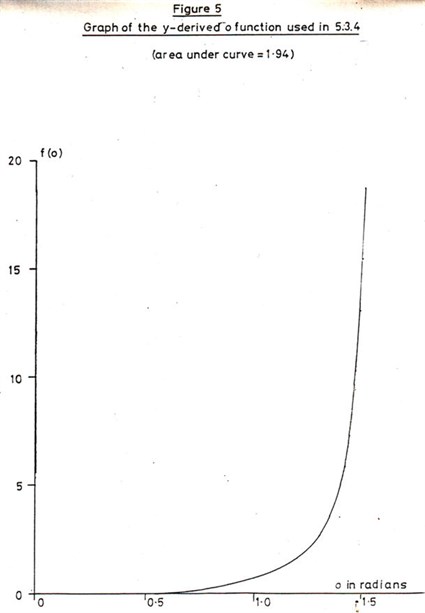
This is simplest evaluated numerically from the area under the curve of the function being integrated, and the limits are chosen to be the start point (o=0) and the value of o at which 1mm separation occurs (o=1.52 radians). Figure 5 shows the function plotted between these limits; numeric substitution using the above equation, voltages of 500V, and the value of the area under the plotted curve gives;-

 E_y = 3 x 10 ^-8 joules

From the earlier analysis, the initial kinetic energy of ball motion can be found from

 

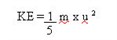
and, if the ball has 0.1 Kg mass and is moving at 5 cm/second, the value of KE is 2 x 10 ^-5. The loss in velocity v/v_o can be found from:-

 

 

 

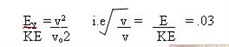
Therefore, approximately 3% of velocity loss is predicted in the last quarter turn. However, if the voltages are doubled, the loss in velocity is similarly doubled; 1KV on both balls could account for 6% loss in spin velocity.

A similar procedure carried out for the x component gives the initial equation:-

   

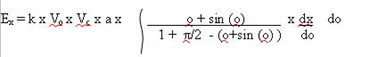
The differential can be readily determined from the previous relation between y and o. and thus ;-

 

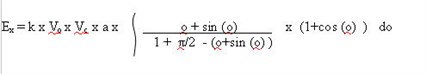
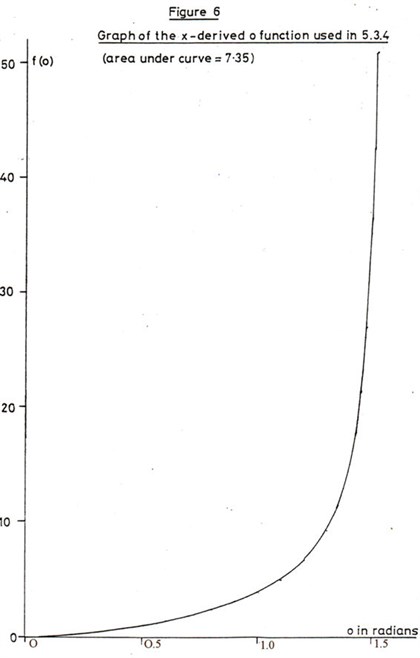
Numeric evaluation of E for voltage values of 500V, in a manner exactly parallel to that of the y component (the function to be integrated is shown in Figure 6) gives the total energy loss as 2 x 10^-7 , and therefore the loss in velocity of this component is evaluated from;-

  

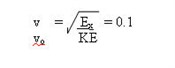
Thus, 500V on each ball gives a 10% loss in spin velocity of the component perpendicular to the main ball rotation. It is interesting to note that if voltage is increased by an order of magnitude, a not impossible situation, this analysis suggests a complete stop of the "side" rotation of the cue ball.

5.3.5 Discussions of effects of the last quarter - turn

This analysis is purely exploratory, and is only intended to give an indication, not a total mathematical description, of the way electrical fields affect ball motion. However, if the above is even approximately a valid model, it is clear that a substantial change occurs in rotational velocity as the balls collide. This is equivalent to an increase in drag or friction qt the collision, and could certainly account for different sound made by the "kick"; according to reports, the impact is much less sharp than that of a normal snooker collision. Further credence to the hypothesis of drastic loss of spin is given by previous experiments (1) increasing friction at the impact point, where a "kick-like" phenomenon occurred.

It must be noted that the change in rotation need not be a decrease; the analysis is of enough generality to be equally valid in the case of a negatively-charged local area passing over a positively - charged spot on the table, and therefore cause an increase in rotational velocity.

 

6. CONCLUSIONS AND RECOMMENDATIONS

6.1 Summary of Electrostatic Effects and their analysis using a simple model

Because the "kick" is an uncommon occurrence, it was not expected that the preceding experimental or theoretical work involving simplified models would indicate its presence. However, a number of possible mechanisms can be postulated from the following conclusions, and all are worthy of further study.

Even in the idealised case of a perfectly rolling ball, with no skidding motion between cue strike and impact of cue ball and object ball, the cue ball will lose up tu 5% of its initial kinetic energy in the process of overcoming electric field repulsion due to the charges in both cue and object balls. Thus is derived from the mathematical analysis of a fairly slow shot in which the initial cue ball velocity is 5cm/second and the voltage on each ball is of the order of 500 Volts. The latter is well within experimentally measured values.

The balls and the table baize are excellent insulators, and the charge is delivered to the cue ball by the cue tip. Thus, although the overall voltage as measured a few centimetres from the ball may be in the 100V - 500V range, a small area of the ball may be at a potential well in excess of 1KV. While the charge distribution and movement when the balls are close to impact are difficult to predict, a simplified analysis of the last quarter turn of the ball before impact indicates the possibility of loss of 10% of at least one of the two possible rotational components of ball motion.

6.2 Charge Transfer Mechanism

The source of the electrical charges given to balls and table is the players involved. As is well known, merely working across certain types of carpet will create a potential; the process of moving an arm may add 100V to this. Indeed, during experimental work, one participant was found to be generating in excess of 1KV during the process of walking from one shot to the next. The two types of cue made available were not resistive enough to prevent transfer of charge to the cue ball. Conversely, the wood of the table was conductive enough to dissipate this change when the players body rested on it in preparation for a shot. Dissipation of charge through the table baize is also too slow to significantly affect any charge placed on the balls in the time scale of the period between shots.

In addition, anecdotal evidence concerning the increased likelihood of the "kick" happening when the black ball is the target may be explained by the fact that in top level play, it is the ball most handled and therefore most likely to absorb electrical charge from the gloves of the referee.

6.3 Charge distribution on the table

The presence of the "track" of residual charge left by a moving ball (and of opposite polarity to that on the ball) was noted during experimental work. Although this charge is an order of magnitude below that of the ball involved, it is evidence that charge transfer is occurring during ball travel.

However, if the track is parallel to the cue ball movement, as often occurs when a player is successively potting red and black balls into one pocket, little or no electrical work is done because the charges are not moving closer together, and the maximum effect expected is a deviation of the order of millimetres at the object ball position. If the line of motion of the cue ball and the line of the track of positive charge cross, the analysis is to a first order similar to that of the last quarter - turn, and about 10% of velocity loss may occur.

6.4 Other Effects

It must be emphasised that the mathematical analyses have, in the interests of simplicity, not considered the following effects which may contribute towards the electrical field effects present in the system.

6.5.1 Frictional motion

In the perfectly general case, the cue ball starts its motion with a period of skidding motion, then settles into pure rolling motion. While it is possible to play a shot with no skid component whatsoever, merely by hitting the cue ball in a certain way, a long-range shot (in which the skidding motion imparts greater accuracy) may cause the first 30% of cue ball movement to be entirely frictional before settling into rotation. Thus, in addition to the charge given to the cue ball by the player, some further charge may be created triboelectrically by this frictional motion. This mechanism is corroborated by the simple experimental test of wiping the ball against a few centimetres of table baize and thereby producing a voltage of 1KV on the ball.

6.4.2 Charged range effects

Since the electric field of the system of two balls is inversely dependent on their separation, it becomes theoretically infinite when contact is made. In practice, the simplistic analysis does not give ludicrously high values of kinetic energy loss if the integration of thus quantity is limited to sensibly close final separations of 1mm or 0.1mm. However, because the predicted asymptotic behaviour is unrealistic, the close range effects of localised charge on both balls and table should be examined both experimentally and theoretically.

6.4.3 Charged table effects

The effects on a charged ball moving across an oppositely charged track have not been considered. It is expected that the effect will be similar in nature but of opposite sign to those produced by the existing analysis of the last quarter-revolution of the ball. This indicates the possibility of an increase in angular velocity as opposed to the decrease predicted in the previous cases. The balance of rotational and skid velocities mat thereby be upset and a skid component produced at the expense of rotational velocity, giving both increased likelihood of frictional generation of charge and of unpredictability of impact due to velocity changes.

In addition, the effect of negatively charged spot on the ball passing directly over a positively charged track left by a previous shot may cause a drastic apparent increase in friction due to the electrical attraction of this system.

6.5 Methods of reducing electrostatic charge effects

Table earthing would accomplish little of use, since the cloth is the site of the problem and is a highly effective insulator. The use of anti-static carpets may alleviate the accumulation of charge by players, but very few carpets exist which are completely reliable in this respect. Anti-static spraying or cleaning agents applied to carpets would possess the disadvantage of periodic treatment, but may provide effective interim solution.

The application of these widely used methods of static control would lower, without entirely removing, the localised charge which this work indicates may be the major source of unpredictability of ball trajectory.

Since the presence of human players almost guarantees the generation of static charge, and ideal measure would be to create a table surface which could easily dissipate electric charge when the player placed a hand upon it. The major disadvantage with this approach is the possibility that the new anti-static surface could have noticeably different playing characteristics not acceptable to top - class players accustomed to the electrostatically-vunerable tables already in use.

Because the analysis indicates that local charge effects may well be of paramount importance in producing the kick, the dissipation of charge on the ball could be an effective solution. Since it is probable that the differences between the ball colours in charge creating and retaining ability are due to either different concentrations or different compositions of the dyes used to colour the resin, a search could be made for dyes with the correct colours, chemical compatibility with the ball material, and electrical resistance reducing properties. In the absence of this, a bulk additive could be found or a surface layer incorporated into the ball to reduce effective charge retaining ability.

To reduce the effect of the player on the cue ball, cues of greater resistance could be used, thereby preventing the main mechanism of charge transfer from operating. This would not remove the triboelectric effect between balls and table, nor would it prevent the referee from charging balls removed from pockets, nor would it prevent the creation of local charge table areas caused by players hands.

APPENDIX  A

REFERENCES

1   "what causes the kick", R. Levi, "The Billiard Player", series of articles Oct, 1923 - Jan. 1924

2    as (1)

3   CRC Handbook of Chemistry and Physics, 56h Edn. , p. A-121

4   "Billiards Mathematically Treated" , G. W Hemming Q.C. , Macmillan 1899

5   "The Mathematics of Snooker" , A. G. Mackie, J. Inst. Math. Applic. Vol. 18 p. 82-89

6   see for example "ESD Protection Test Handbook", Keytek Instrument Corp.

In addition to these specific documents, all of the mathematical techniques used may be found in any introductory undergraduate text. This is also true for all of the electrical physics used.

APPENDIX  B

BASIC programs used in evaluation of analyses

The following programs were used on a sharp computer PC-1246. Due to memory restrictions, little user friendliness has been incorporated.

1.  program used to evaluate velocity loss in 5.3.2

10 M = 0.1

20 A = 0.03

30 R = 8.85 * (10^ -12) : R=R*4

40 INPUT "CUEBALL VOLTS";W

50 INPUT "OBJECTBALL VOLTS";V

60 INPUT "SEPARATION";S

80 INPUT "FINAL DISTANCE";D

90 INPUT "START VELOCITY";U

100 K = 4 * PI * R * A * 5 / (M * U * U)

110 F = D + (S * LN ( ( S-D/S) )

120 Z = SQR (1- (K * V * W * F) )

130 Z = 1 - Z

140 PRINT Z

150 END

2. Program used to evaluate x function used in 5.3.4

200 INPUT O: P = O * 57.3

210 A = O + SIN (P)

220 B = 1 + COS(P)

230 C = 1 + (PI/2); C = C - A

240 D = A * B / C: PRINT D

240 GOTO 200

(n.b - the computer used could not evaluate trigonometric functions in radians, so the variable P is simply O converted from radians to degrees)

3.  Program used to evaluate the y function used in 5.3.4

400 INPUT O: O = O * 57.3

410 A = 1 - COZ (O)

420 B = TAN (O)

430 C = A * B: PRINT C

440 GOTO 400

(n.b - O converted to radians for the reason given above)

© 1987-2013 -E.A. Clare & Son Ltd.

       Additional pictures taken in 1987 during the experiments (all picture copyright of       E.A. Clare & Son Ltd & Peter Clare):-

 

Norman Clare is on the right of the picture

 

 

 

© 1987-2013 -E.A. Clare & Son Ltd.

This article and picture is the copyright of E. A. Clare & Son Ltd. and can not be used as a whole of in part without the permission of E. A. Clare & Son Ltd. and when permission granted acknowledgement of the source clearly must be given.

© E.A. Clare & Son Ltd. 2018. © Peter N. Clare 2018
Reproduction of this article allowed only with the permission from E.A. Clare & Son Ltd.

eshop - thurston.co.uk

email - thurston@eaclare.co.uk

phone - +44 (0)151 482 2700